CompLearn Example: Discovering Meaning Through Google

The following example creates a distance matrix of NGDs (Normalized Google Distance) from a term list of numbers and colors. This list list is also included with the software. Read more about NGD in Automatic Meaning Discovery Using Google.

Step 1: Create a Distance Matrix

$ ncd -b -g -t examples/colors-nums.txt examples/colors-nums.txt

This creates a square distance matrix using the string literals in the file examples/colors-nums.txt. With the -b option, a binary file called distmatrix.clb will be created by default. The -g tells ncd to generate NGDs using the "Google compressor." The resulting matrix is output to stdout.

Step 2: Create a Tree

$ maketree distmatrix.clb

Here, we use the previously created distance matrix to create an unrooted binary tree. The resulting tree is output as a .dot file called treefile.dot by default. The contents of the resulting .dot file describe how the nodes of the tree are connected and how they are labeled. Please note: because we are generating a tree from a medium sized matrix (21x21), maketree may take a few hours to complete. However, feel free to take a peek at treefile.dot while it is still in progress.

Step 3: Lay Out Your Tree

$ neato -Tps -Gsize=7,7 treefile.dot > colors-nums-unrooted.ps

This neato command will create a visual representation of your tree in postscript format. This particular postscript file is laid out on a 7x7 inch drawing area.

If instead you prefer a browser-compatible format, such as .png you can use the following command.

$ neato -Tpng treefile.dot > colors-nums-unrooted.png

neato supports other popular formats such as .jpg and .gif.

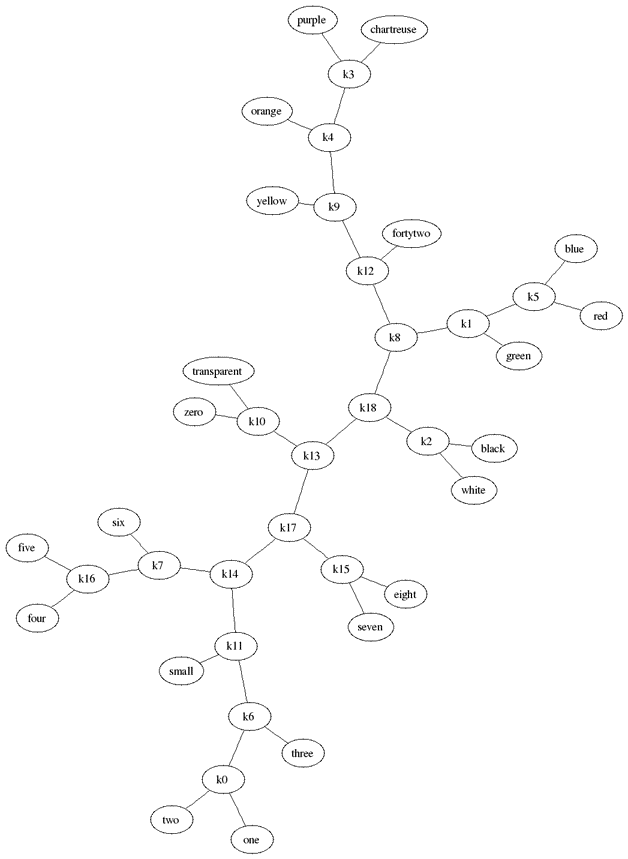
Step 4: Analyze Your Results

As you can see in the resulting tree below, numbers and colors cluster together despite the lack of any prior knowledge of which category a term belongs. Notice also that "red," "blue," and "green," the primary colors of light, are cozy on their own little branch. "Black" and "white," unsurprisingly, are paired together. Perhaps most interesting of all, however, is the grouping of "small," which itself is not a number, with the quantitatively smallest numbers in the tree.